3.3.3 Canonify

Canonify is a more comprehensive form of simplification. While simplification is often focused on a small subject, canonify is always applied to the entire active expression. And while simplification commutes only constants to arrange them together, canonify rearranges all the terms into a unique configuration called a canonical form.

Canonify treats formulae, definitions and equations in slightly different ways. If the active expression is a formula, canonify behaves as described above. If it is a definition, canonification is applied to the elaboration. If it is an equation, canonification is applied to each side independently.

Canonify also treats Boolean expressions differently from polynomials. Boolean expressions are canonified by applying a Boolean simplification algorithm.

3.3.3.1 Polynomial canonification

Canonify reorders product terms (operands of additive operators) so that any constant comes first, followed by variables in ascending order by name and descending order by exponent. Within each reordered term, constants are combined by multiplication and variables with the same name are combined by adding their exponents. Terms that differ only in the constant are combined by addition.

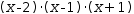
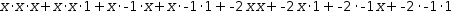
To see Canonify in action, Distribute (x-2)⋅(x-1)⋅(x+1) twice to produce a long complicated expression. Try to simplify the expression manually by rearranging terms and simplifying subexpressions. Then start from the original distributed form and apply Canonify . Thus

x⋅x⋅x+x⋅x⋅1+x⋅-1⋅x+x⋅-1⋅1+-2⋅x⋅x+-2⋅x⋅1+-2⋅-1⋅x+-2⋅-1⋅1

becomes

x^3-2⋅x^2-x+2.

For practice, distribute, then canonify the following expressions.

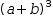
(a+b)^3
(b+a)^3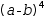
(a-b)^4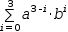
∑0, 3, a^(3-i)⋅b^iⅆi

3.3.3.2 Boolean canonification

A canonical form of Boolean expressions is produced by finding the essential prime implicants of the expression along with additional implicants to cover the expression. An expression is Boolean if it consists of the usual Boolean operators, the relational operators, real variables and real values.

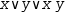
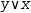
For example, inclusive-or is given by x∨y∨x∧y. After canonification, the expression is y∨x.

At this point, it is not possible to specify “don't cares” to the canonification algorithm.